A maioria das noções em Matemática são definidas utilizando outras noções que já foram estabelecidas. Assim, para definirmos uma noção, precisamos de outra préestabelecida, para esta outra, precisamos de mais outra, etc… Aí surge a pergunta natural: E a primeira de todas as noções, como é estabelecida?
É natural que esta primeira noção não possa ser definida usando-se outra préestabelecida, de onde concluímos que não podemos definir tudo. Somos obrigados, ao iniciar o estudo de um certo conteúdo matemático, adotar, sem definir, as primeiras noções, que são chamadas noções primitivas.
Isto foi o que Euclides (330 a.C. a 270 a.C. ) fêz com a Geometria quando escreveu “Os Elementos”, onde alguns axiomas foram admitidos e tudo o mais foi deduzido a partir deles.
Na teoria dos conjuntos adotamos duas noções primitivas, a saber, a de conjunto e a de pertinência, denotada por ∈.
A segunda noção estabelece uma relação entre conjuntos da seguinte forma: se x e A são conjuntos, a expressão x ∈ A pode ser lida como “x pertence a A” ou “x está em A”. Com esta noção podemos definir a noção de elemento, da seguinte forma:
Definição 2.1. Seja x um conjunto. Se existe um conjunto A tal que x ∈ A, então x é dito ser elemento, ou seja, dizemos que x é um elemento de A, ou ainda que x pertence a A.
Quando um conjunto x não for um elemento do conjunto A, escrevemos x 6∈ A, e lemos “x não pertence a A”, ou ainda “x não está em A”, que é a negação de x ∈ A.
Parece estranho escolhermos conjunto e pertinência como elementos primitivos ao invés de conjunto e elemento, mas é mais fácil definir elemento usando a noção de pertinência do que definir a noção de pertinência usando a noção de elemento.
Estabeleceremos como convenção o uso de letras maiúsculas para denotar conjuntos e letras minúsculas para denotar elementos.
A seguir definimos a noção de igualdade de conjuntos.
Definição 2.2. Sejam A e B conjuntos. Dizemos que o conjunto A é igual ao conjunto B, e denotamos por A = B, se todo elemento de A é um elemento de B e vice-versa. Simbolicamente escrevemos
A = B ⇐⇒ (∀x)[(x ∈ A −→ x ∈ B) ∧ (x ∈ B −→ x ∈ A)].
Note que, com esta definição, dois conjuntos são iguais se, e somente se, eles têm os mesmos elementos.
A nosso intuição nos diz que quando um elemento x está em um conjunto A e x é igual a outro elemento y, então é natural esperar que y também seja elemento de A; isso é garantido pelo primeiro axioma da teoria dos conjuntos.
Axioma da Extensão: Se x = y e x ∈ A, então y ∈ A.
A seguir definimos a noção de inclusão de conjuntos.
Definição 2.3. Sejam A e B conjuntos. Dizemos que A está contido em B, (ou B contém A) e denotamos por A ⊆ B(ou B ⊇ A), se todo elemento de A for um elemento de B. Neste caso, dizemos também que A é um subconjunto de B. Simbolicamente escrevemos
A ⊆ B ⇐⇒ (∀x)(x ∈ A −→ x ∈ B).
Se A ⊆ B e A é diferente de B, dizemos que A é um subconjunto próprio de B e denotamos por A B ou A ⊂ B.
Estas noções, definições e axioma, nos permitem demonstrar o seguinte resultado:
Proposição 2.4. Sejam A,B e C conjuntos. Então as seguintes propriedades são válidas:
- Reflexiva: A = A.
- Simétrica: A = B =⇒ B = A.
- Transitiva: (A = B) ∧ (B = C) =⇒ A = C.
- Reflexiva: A ⊆ A.
- Anti-simétrica: A ⊆ B ∧ B ⊆ A ⇐⇒ A = B.
- Transitiva: (A ⊆ B) ∧ (B ⊆ C) =⇒ A ⊆ C.
Prova: Vamos mostrar alguns ítens; a demonstração dos restantes fica como exercício.
- A proposição x ∈ A −→ x ∈ A é uma tautologia, logo, da Definição 2.2, temos A = A.
- Da Definição 2.2 temos que A = B ⇐⇒ (∀x)[(x ∈ A −→ x ∈ B) ∧ (x ∈ B −→ x ∈ A)]. Agora, pela comutatividade do conectivo ∧ e novamente pela Definição 2.2, concluímos que B = A.
(e) Da Definição 2.3, temos que A ⊆ B ∧B ⊆ A é equivalente a proposição (∀x)[(x ∈ A −→ x ∈ B) ∧ (x ∈ B −→ x ∈ A)], que por sua vez, é equivalente a A = B pela
Definição 2.2:
Uma maneira de representar um conjunto é exibir seus elementos entre chaves e separados por vírgulas, mas podemos também caracterizar um conjunto através de uma propriedade que o defina. Isso deve ser feito axiomaticamente, tomando certos cuidados para evitar contradições. Vejamos o axioma que nos permite construir conjuntos a partir de propriedades.
Axioma da especificação: Sejam A um conjunto e p(x) uma proposição em x que deve ser expressa totalmente em função dos símbolos ∧, ∨, ∼, −→, ∈, ∃, ∀, [] e variáveis x,y,z,… ,A,B,C,…. Então existe um conjunto que consiste de todos os elementos x de A que tornam p(x) verdadeira. Simbolicamente, escrevemos
{x ∈ A; p(x) é verdadeira}.
Observação 2.5. A restrição de p(x) utilizar somente símbolos lógicos e variáveis faz sentido para evitar paradoxos do tipo semântico. Um exemplo disso é o seguinte paradoxo, que numa versão simplificada, diz: Paradoxo de Richard: Todo número inteiro pode ser descrito em palavras utilizando um certo número de letras. Por exemplo, o número 36 pode ser descrito como “trinta e seis” ou “quatro vezes nove”. A primeira descrição utiliza 11 letras e a segunda 15 letras. Vamos dividir o conjunto dos números inteiros positivos em dois grupos, o primeiro contendo todos os números inteiros positivos que podem ser escritos com no máximo 100 letras e o segundo inclui todos os números inteiros positivos que necessitam de pelo menos 101 letras para descrevê-los. Há um número finito de números no primeiro grupo, pois existem no máximo 24100 expressões com no máximo 100 letras. Existe então um menor inteiro positivo no segundo grupo. Este menor inteiro pode ser descrito pela frase “o menor inteiro que não é descrito com menos de 100 letras”, o que o descreve com menos de 100 letras. Então este número pertence ao primeiro grupo, o que é uma contradição.
Note que este conjunto não pode ser construído pelo axioma da especificação, pois a propriedade do axioma está restrita a operadores lógicos e alguns símbolos. Por isso estamos livres desta contradição.
Observação 2.6. Outra aplicação mais interessante deste axioma é que ele garante que não existe um conjunto que contenha todos os conjuntos.
De fato, supondo que exista o conjunto cujos elementos sejam todos os conjuntos, seja U tal conjunto. Assim, usando o axioma da especificação, podemos formar o conjunto B = {x ∈ U; x /∈ x}. A questão agora é: será que B ∈ U?
Se sim, temos duas possibilidades, B ∈ B ou B /∈ B.
Se B ∈ B, pela especificação de B, temos que B /∈ B e, se B /∈ B, então B ∈ B, o que é uma contradição. Assim, chegamos à conclusão que B /∈ U, ou seja, não existe um conjunto universo. O argumento que levou a essa conclusão chama-se o paradoxo de Russel, cuja versão popular é: Numa certa cidade existe um barbeiro que só faz a barba nos homens que não barbeiam a si próprios. Quem faz a barba do barbeiro?
Com o auxílio do axioma da especificação, podemos construir vários conjuntos importantes.
Definição 2.7. O conjunto vazio, denotado por ∅, é o conjunto que não possui elemento algum.
A existência deste conjunto é garantida pelo axioma da especificação, pois dado qualquer conjunto A, temos que ∅ = {x ∈ A; x 6= x}.
Definição 2.8. Sejam A e B dois conjuntos. A união de A e B, denotada por A∪B, é o conjunto formado pelos elementos x tais que x está em pelo menos um dos dois conjuntos A ou B. Simbolicamente,
A ∪ B = {x;x ∈ A ∨ x ∈ B}.
A intersecção de A e B, denotada por A∩B, é o conjunto formado pelos elementos x tais que x está em ambos os conjuntos A e B. Simbolicamente,
A ∩ B = {x;x ∈ A ∧ x ∈ B}.
Dessa definição, temos as seguintes equivalências lógicas:
x ∈ A ∪ B ⇐⇒ (x ∈ A ∨ x ∈ B)
e
x ∈ A ∩ B ⇐⇒ (x ∈ A ∧ x ∈ B).
Note que a existência dos conjuntos A ∪ B e A ∩ B é garantida pelo axioma da especificação.
Com relação à união e à intersecção de conjuntos temos as seguintes propriedades:
Teorema 2.9. Sejam A e B conjuntos. Então:
(a) A ⊆ A ∪ B e B ⊆ A ∪ B. (b) A ∩ B ⊆ A e A ∩ B ⊆ B.
- A ⊆ B ⇐⇒ A ∪ B = B e A ⊆ B ⇐⇒ A ∩ B = A.
- A ∪ (B ∩ A) = A e A ∩ (B ∪ A) = A.
Prova: Para os ítens (a) e (b), mostraremos uma das inclusões, as outras são demonstradas de forma análoga e ficam como exercício.
Vamos mostrar que A ⊆ A ∪ B, o que é equivalente, por definição, a mostrar que x ∈ A =⇒ x ∈ A ∪ B, o que é equivalente a mostrar que x ∈ A −→ x ∈ A ∨ x ∈ B é uma tautologia , o que é verdade, pois é uma implicação do tipo p −→ p ∨ q.
No ítem (c), também provaremos somente uma das equivalências, ficando a outra como exercício.
Vamos mostrar que A ⊆ B ⇐⇒ A∪B = B. Como (p ⇐⇒ q) ⇐⇒ (p =⇒ q)∧(q =⇒
p), vamos mostrar as implicações =⇒ e ⇐= separadamente.
(=⇒) Queremos mostrar que se A ⊆ B, então A ∪ B = B. Note que pela igualdade de conjuntos, temos que mostrar que A ∪ B ⊆ B e B ⊆ A ∪ B. A segunda inclusão segue de (a). Para a primeira, seja x ∈ A ∪ B, então, x ∈ A ∨ x ∈ B. Se x ∈ A, como por hipótese, A ⊆ B, temos que x ∈ B. Assim, x ∈ B, em ambos os casos, como queríamos.
(⇐=) Se A ∪ B = B, então, como A ⊆ A ∪ B = B, temos claramente que A ⊆ B.
A demonstração do ítem (d) fica como exercício.
Dizemos que dois conjuntos A e B são disjuntos se eles não possuem elementos em comum, ou seja, se A ∩ B = ∅.
Teorema 2.10. Sejam X,A e B conjuntos. Então temos:
- ∅ ⊆ A, A ∪ ∅ = A e A ∩ ∅ = ∅.
- X ⊆ A ∪ B ⇐⇒ X ⊆ A ∨ X ⊆ B e X ⊆ A ∩ B ⇐⇒ X ⊆ A ∧ X ⊆ B.
Prova: Vamos mostrar a primeira inclusão do ítem (a), ou seja que ∅ ⊆ A. Por definição, temos que mostrar que x ∈ ∅ =⇒ x ∈ A. Como a proposição p : x ∈ ∅ é sempre falsa, então p −→ q é verdadeira para qualquer proposição q, o que mostra a inclusão. Outra maneira de mostrar este fato é usando-se a contra-positiva, isto é, supondo que x /∈ A, então certamente temos que x /∈ ∅, pois o conjunto vazio não contém elementos, assim, x /∈ A =⇒ x /∈ ∅.
Mostremos agora a equivalência X ⊆ A ∩ B ⇐⇒ X ⊆ A ∧ X ⊆ B, deixando as restantes como exercício.
(=⇒) Nesta implicação, a hipótese é X ⊆ A ∩ B e a tese é X ⊆ A ∧ X ⊆ B. Seja x ∈ X; como por hipótese X ⊆ A ∩ B, temos que x ∈ A ∩ B e, pela definição de intersecção, temos que x ∈ A ∧ x ∈ B. Portanto X ⊆ A ∧ X ⊆ B.
(⇐=) Nesta implicação, a hipótese é X ⊆ A∧X ⊆ B e a tese é X ⊆ A∩B. Seja x ∈ X; por hipótese x ∈ A∧x ∈ B e, pela definição de intersecção, temos que x ∈ A∩B. Portanto X ⊆ A ∩ B.
Diagramas de Venn e de Linha
Uma maneira simples de ilustrar as relações entre conjuntos é por meio de diagramas. Existem dois tipos mais utilizados, que são os diagramas de Venn e os diagramas de linha.
No diagrama de Venn os conjuntos são representados por regiões limitadas do plano e suas relações são representadas pelas posições dessas regiões. Nas figuras abaixo, representamos algumas relações entre os conjuntos A e B.
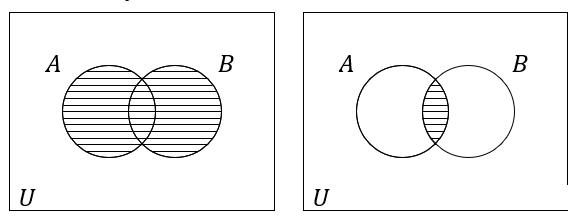
(a)A∪B (b)A∩B
Figura 2.1: União e interseção de conjuntos.
No diagrama de linha, não representamos os conjuntos mas sim a relação de inclusão entre eles. Um conjunto que contém o outro conjunto estará num nível vertical acima ligado ao primeiro por um segmento de reta. Caso os conjuntos não possuam a relação de inclusão, eles não são unidos pelo segmento de reta. Neste caso, eles são colocados horizontalmente, em posições diferentes. Na figura abaixo vemos um exemplo de um diagrama de linha.
B
A
>>>>
C D